LPR research courses computer misc persons info www


Der Z-Buffer

Dieses Dokument verwendet Sprachdefinitionen von HTML-3.0 (Hoch- und Tiefstellung). Eine Verwendung von Netscape 2.0 oder höher ist daher zu empfehlen.


1. Der Z-Buffer Algorithmus

Das Z-Buffering stellt ein Bildraum-Verfahren für dir Sichtbarkeitsberechnung von 3-dimensionalen Körpern dar. Neben diesem Z-Buffering exisitieren weitere Methoden für eine Sichtbarkeitsberechnung.
Die Objektraum-Verfahren erzeugen ebenfalls 2-dimensionale Darstellungen eines Körpers. Dabei werden die Koordinaten eines Körperelements allerdings nicht in rasterisierter Form wie bei den Bildraumverfahren verwendet. Dadurch kann die Berechnung des Bildes innerhalb der maschinengenaugkeit beliebig genau bleiben. Für die Sichtbarkeitsberechnung kommen Verfahren zur Sortierung der Listen nach bestimmten Kriterien zur Anwendung.
Ein weiteres verfahren ist das Listenprioritäts-Verfahren, eine Mischung aus dem Bildraum- und dem Objektraum-Verfahren. Die Elemente werden für eine Sichtbarkeitsprüfung zunächst sortiert (Objektraum-Verfahren) und anschließend für den Vergleich mit anderen bereits eingetragenen Elementen rasterisiert (Bildraum-Verfahren).

Für eine Fläche ergibt sich bei der Rasterisierung und der Berechnung der Tiefenwerte für einen Flächenpunkt ein erheblicher Rechenaufwand. Um die Anzahl der zu bearbeitenden Flächen möglichst gering zu halten, werden Verfahren verwendet, um Flächen auszusondern, die für die Sichtbarkeitsberechnung nicht relevant sind.
Die einfachste Methode stellt das Backface-Culling dar, durch das die Rückseiten von Körpern verworfen werden. Dieser Fall liegt dann vor, wenn der aus dem Körper herauszeigende Normalenvektor einer Fläche nicht in die Richtung der Kamera zeigt. Diese Methode erfordert den wenigsten Rechenaufwand und verwirft eine große Anzahl von Flächen (über 50%), und findet daher als allererstes Verfahren zur Reduktion der Flächenzahl Verwendung.
Weiterhin werden die Flächen an den Begrenzungen des sichtbaren Bereiches des Z-Buffers geclippt. Dabei werden die Flächen zum einen in ihrer Ausdehnung begrenzt, d.h. nicht sichtare Bereiche werden abgeschnitten, oder zum anderen werden im Ganzen nicht sichtbare Flächen verworfen. Dazu werden die Koordinaten der Eckpunkte aus dem lookalen Koordinatensystem in das Bildschirm-Koordinatensystem transformiert. In der 2-dimensionalen Bildschirmebene erfolgt nun das Clippen. Es ist erschichtlich, daß dieses Verfahren einen erhöhten Rechenaufwand bedarf. Dies ist ein weiterer Grund für das oben angesprochene Backface-Culling.
Nachdem sichergestellt ist, daß nur die sichtbaren Bereiche einer Fläche in die Sichtbarkeitsberechnung einfliessen, kann die Fläche gerendert werden. Dies wird dadurch erreicht, daß alle Flächen eines Körpers in die 2-dimensionale Bildschirmebene eingetragen werden. Zudem wird für jeden Punkt der Fläche dessen Tiefenwert (Z-Wert) berechnet. Dazu in zwei korrespondierenden Frames (Z- und Id-Frame) die Tiefen- und Id-Werte gespeichert. Die Id einer Fläche ergibt sich dabei automatisch durch eine fortlaufende Nummerierung aller eingetragenen Flächen. Bei der Sichtbarkeitsberechnung wird nun für einen Flächenpunkt dessen Z-Wert mit dem im Z-Frame gespeicherten Wert verglichen. Ist der Z-Wert des Flächenpunktes kleiner, so bedeutet dies per Definition, daß der Flächenpunkt näher als ein bereits vorhandener Flächenpunkt ist und somit sichtbar ist. Sodann wird der neue Id-Wert in den Id-Frame und der neue Z-Wert in den Z-Frame eingetragen und der Flächenpunkt als sichtbar markiert.

Wurden alle notwendigen Flächen in den Z-Buffer eingetragen, besteht daraufhin die Möglichkeit in einem weiteren Schritt Merkmale auf ihre Sichtbarkeit hin zu überprüfen. Als Ergebnis dieses Testes werden die sichtbaren Teile eines Merkmales zurückgeliefert.

Wie bereits angedeutet, werden für den Z-Buffering-Algorithmus verschiedene Transformationen verwendet. Zum einen wird das Kamerakoordinatensystem verwendet, welches durch die Kamera erzeugt wird. Aus dem Kamerakoordinatensystem werden die Eckpunkte, dann in das Bildschirmkoordinatensystem übergeführt. Die Orientierungen und Definitionen der Koordinatensysteme werden im folgenden verdeutlicht.

Die beiden nachfolgenden Abbildungen zeigen Darstellungen des Z- und Id-Frames. Im Z-Frame wird dabei die Tiefeninformation Grauwerte umgesetzt. Punkte die näher zum Betrachter sind, werden dabei in einem helleren Farbton angezeigt. Die Farbe Blau stellt desweiteren die "Unendlichkeit" dar. Im Id-Frame werden die Flächen in unterschiedlichen Farben dargestellt.


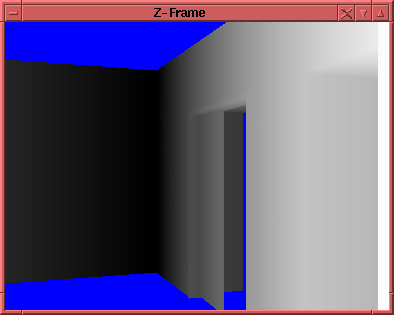
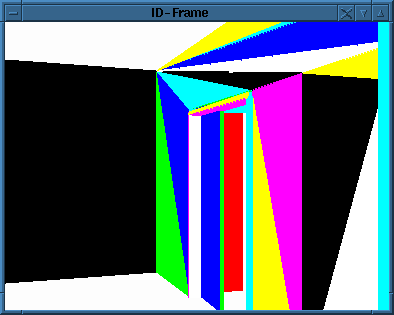
Abbildung 1.1: Darstellungen des Z- und Id-Frames

2. Koordinatensysteme

2.1 Kamerakoordinatensystem

Das Kameraoordinatensystem wird durch die Position der Kamera in der Welt definiert. Es wird dabei das Koordinatensystem nach Lenz (Lenz87) verwendet.
Der Brennpunkt der Kamera definiert dabei den Ursprung des Kamerakoordinatensystems. Die z-Achse der Kamera zeigt dabei direkt in deren Sichtrichtung. Dadurch ergibt sich automatisch aus dem z-Wert eines Objektes dessen Entfernung von der Kamera, die für den z-Buffer-Algorithmus notwendig ist. Die beiden anderen Achsen wurden so angeordnet, daß sich eine Übereinstimmung mit den üblichen Koordinatensystemen von Bildschirmen ergibt. (X' und Y' in Abbildung 2.2.) Dies bedeutet die y-Achse zeigt nach unten, die x-Achse nach rechts.


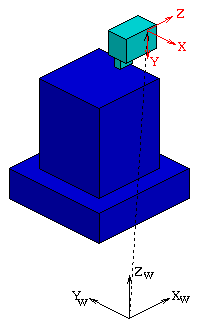
Abbildung 2.1: Kamerakoordinatensystem

Die untenstehende Tabelle 2.1 zeigt die einzelnen Schritte, die notwendig sind, um die Transformationsmatrix zu erstellen, welche die Transformation eines Punktes aus den Welt- in Kamerakoordinaten vollführt.

SchrittRotationsachseTranslationsvektorWertMatrix-Manipulation
Rotationz-Achse--90°Multiplikation mit DZ(-90°)
Rotationy-Achse-90°Multiplikation mit DY(90°)
Rotationx-Achse-RollMultiplikation mit DX(Roll)
Rotationy-Achse-ElevationMultiplikation mit DY(Elevation)
Rotationz-Achse-AzimuthMultiplikation mit DZ(Azimuth)
Translation-Ursprungsvektor-Addition von T(Ursprung)
Invertieren---Invertieren der Matrix
Tabelle 2.1: Erstellung der Transfomationmatrix

2.2 Bildschirmkoordinatensystem

Für das Füllen des Polygons und den Z-BufferingAlgorithmus müssen die Koordinaten der Eckpunkte aus dem Kamerakoordinatensystem in das Koordinatensystem der Bildebene transformiert werden. Es wird dabei aus dem 3-dimensionalen Kamerakoordinatensystem in das 2-dimensionale Bildschirmkoordinatensystem transformiert. Die Bildebene wird parallel zur x-y-Ebene und den Punkt (0, 0, 1) auf der z-Achse schneidend festgelegt. Die Geometrie der Bildebene wird durch weitere verschiedene Parameter definiert. Dazu zählen die Abstände des Punktes (0, 0) der Bildebene vom Schnittpunkt mit der z-Achse, die Parameter ox und oy. Weiterhin zählen die Pixelabmessungen sx und sy dazu. Die Auflösung des Z-Buffers wird durch die Parameter dx und dy angegeben. Die folgende Abbildung 2.2 verdeutlicht die Bedeutung der einzelnen Parameter und die Orientierung der Koordinatensysteme.


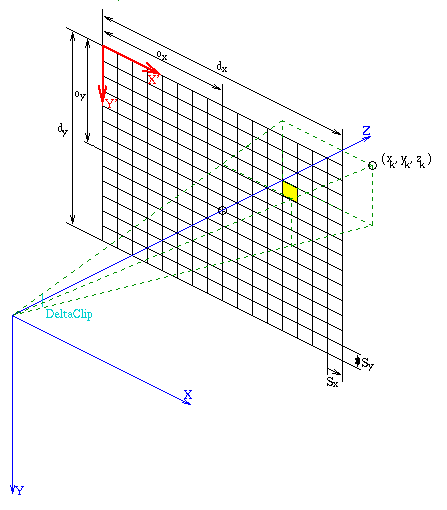
Abbildung 2.2: Bildschirmkoordinatensystem

Für die Transformation in das Bildschirmkoordinatensystem werden die fogenden Formeln verwendet:

yk
yB = ----- + ox
zk·sx

xk
xB = ----- + oy
zk·sy

Der Index k zeigt dabei an, daß die entsprechende Komponente in Werten des Kamerakoordinatensystem vorliegt. Der Index B hingegen zeigt an, daß die Komponente im Bildschirmkoordinaten system vorliegt.

3. Flächenfüllen

Bevor eine Fläche gezeichnet wird, muß die Fläche einigen Tests einigen Tests unterzogen, die ihre Sichtbarkeit bestimmen. Wurde die Fläche als sichtbar erkannt, kann sie rasterisiert werden. Dazu müssen diejenigen Punkte gefunden werden, die sich im Inneren der, auf die Bildebene projezierten Fläche, befinden. Zu diesem Zweck wird die Fläche in horizontaler Richtung unterteilt. Für jede der horizontalen Zeile, der Scanzeile, müssen die beiden äußersten Punkte der Scanzeile gefunden werden. Dies geschieht durch die Rasterisierung des Flächenumrisses und dem Eintragen aller seiner Punkte durch den Vergleich gegen einen Minimal- und Maximalwert. Nachdem die Extrempunkte einer Scanzeile gefunden wurden, sind die Punkte des sogenannten Spans bestimmt und deren z-Wert kann berechnet werden.
Für die Berechnung des z-Wertes wird ein Verfahren verwendet, wie es im folgenden Abschnitt 3.1 beschrieben ist. Der Berechnete z-Wert wird darauffolgend mit dem entsprechenden z-Wert des Punktes im Z-Frame verglichen. Ist der berechnete Wert kleiner, so bedeutet dies, daß der Flächenpunkt näher als ein bereits eingetragener Flächenpunkt ist. Der neue Flächenpunkt ist somit sichtbar und der neue z-Wert wird in den Z-Frame und der Id-Wert der Fläche wird in den Punkt des Id-Frames eingetragen.
Anschließend an das Füllen der rasterisierten Fläche wird der Umriß der Fläche erneut gezeichnet. Dies ist notwendig um zu gewährleisten, daß bei einer anschließenden Merkmalsprädiktion eindeutige Tiefenwerte für die Flächenkanten vorhanden sind. Dazu werden die Kantenpunkte mit einem neuen z-Wert belegt, deren Id-Wert der der Fläche entspricht. Die Tiefenwerte der Linie wird nach dem in Abschnitt 3.2 beschriebenen Verfahren berechnet.

3.1 Berechnung der Tiefe eines Polygonpunktes

Beim Füllen des Polygons in der Bildebene muß für jeden Polygonpunkt dessen Tiefenwert berechnet werden. Zu diesem Zweck wird durch jeden Punkt des Polygons in der Bildebene ein Strahl durch das entsprechende Pixel geschickt und der Schnittpunkt ermittelt. Der Abstand würde sich anschließend aus dem Abstand des Schnittpunktes zum Ursprung ergeben, d.h a = sqrt( sx·sx + sy·sy + sz·sz ). Was aber lediglich von Interesse ist, ist das Verhältnis des Schnittpunktvektors (a·s in Abbildung 3.1) zum Strahlvektor (s in Abbildung 3.1).
Wie dieses Verhältnis berechnet wird, zeigen die Gleichungen in Anschluß an Abbildung 3.1.


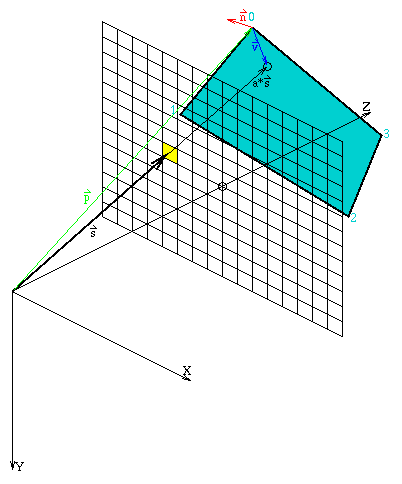
Abbildung 3.1: Berechnung der Tiefe eines Polygonpunktes

v·n = 0,    v = a·s-p
(a·s-p)·n = 0
a·s·n-p·n = 0

p·npx·nx+py·ny+pz·nz
a = ---=---------------
s·nsx·nx+sy·ny+sz·nz

Diese Formel scheint auf den ersten Blick einen hohen Aufwand an Berechnungen nach sich zu ziehen. Es lassen sich jedoch auf einfache Weise Vereinfachungen durch Vorausberechnungen finden, mit denen der Rechenaufwand wesentlich gesenkt werden kann.
So ändert sich der Zähler innerhalb der Fläche nicht, er muß daher für jede Fläche nur einmal berechnet werden.
Bei genauerer Betrachtung des Nenners ergeben sich ebenfalls Teilterme, welche sich nur unter bestimmten Bedingungen ändern.
So ändert sich der letzte Teilterm sz·nz innerhalb der Fläche nicht, da sz immer den Wert 1.0 besitzt. Der mittlere Teilterm sy·ny ändert sich nur für jede Zeile, während sich der erste Teilterm sx·nx nur für jede Spalte ändert. Da das Polygon Zeilenweise abgetastet wird, können die beiden letzten Teilterme für jede Zeile berechnet werden, und nur der erste Teilterm muß immer wieder berechnet werden.

3.2 Berechnung der Tiefe eines Linienpunktes

Bei der Berechnung der Tiefe eines Linienpunktes wird ähnlich verfahren, wie bei der Berechnung der Tiefe eines rasterisierten Polygonpunktes. (Siehe Kapitel 3.1) Für diese Art der Tiefenberechnung ist ein Normalenvektor notwendig. Da es bei einer Linie keinen Normalevektor wie bei einer Fläche gibt, wird der Vektor so gewählt, daß er in Richtung des Betrachters (Kameraursprung) zeigt. Die nachfolgende Abbildung zeigt schematisch wie dies erreicht wird.


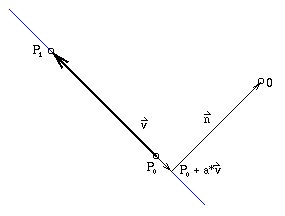
Abbildung 3.2: Berechnung des Normalenvektors einer Linie

Zur Berechnung eines auf die Linie senkrecht stehenden Vektors wird der Punkt gesucht, der den geringsten Abstand zum Ursprung hat. Dieses Minimale Abstand tritt auf, wenn die Linie vom Ursprung (O) zu einem Punkt [O - (P0+a*v)] auf der Linie senkrecht steht. Dies bedeutet, daß das Skalarprodukt aus dem Richtungsvektors der Geraden und der Verbindungsgeraden gleich Null ist. Durch geeignete Umformungen kann dann der Skalierungsfaktor a berechnet werden:

v·(O - (P0 + av)) = 0
(O - P0)·v + av·v = 0

(O - P0)·v
a = --------
v·v

Mit diesem Skalierungsfaktor kann jetzt der Normalenvektor n einfach bestimmt werden:

n = O -  (P0 + av)

Unter der Vorraussetzung, daß der Punkt O gleich dem Ursprung des Lokalen Systems ist, vereinfachen sich die obigen Gleichungen nochmals.


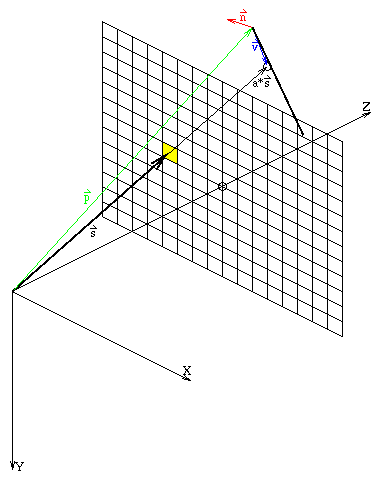
Abbildung 3.3: Berechnung der Tiefe eines Linienpunktes

Für die Berechnung des z-Wertes des Linienpunktes wird die selbe Formel für a verwendet, wie in Kapitel 3.1 gezeigt:

p·npx·nx+py·ny+pz·nz
a = ---=---------------
s·nsx·nx+sy·ny+sz·nz

Im Prinzip können die gleichen Vereinfachungen angewendet werden, wie sie für das Polygon gezeigt wurden. Es muß lediglich unterschieden werden, in welcher Form die Linie gezeichnet werden muß. Besitzt die Linie eine Steigung < 1, d.h. dx > dy, dann wird der Teilterm sy·ny + sz·nz vorausberechnet und nur für jede Änderung der y-Koordinate der Linie geändert. Ist die Steigung der Linie hingegen > 1, so wird der Teilterm sx·nx + sz·nz vorausberechnet und entsprechend nur für Änderungen der x-Koordinate der Linie neu berechnet.

3.3 Clippingverfahren zur Begrenzung der Flächenausdehnungen

3.3.1 Clippen gegen parallele Ebene

Das Clippen gegen eine zur Projektionsfläche parallelen Ebene wird dann angewendet, wenn ein oder mehrere Eckpunkte einer Fläche hinter der Kamera liegen, d.h. die z-Koordinate des Eckpunktes kleiner als Null ist. In diesem Fall wird aber nicht der Wert Null verwendet, sondern der Abstand DeltaClip > 0 zur x-y-Ebene. Dieser Wert verhindert, daß bei der Projektion eine Division durch Null auftritt, da Werte für z immer größer oder gleich DeltaClip sind. Zu diesem Zweck wird die Fläche gegen die zur Projektionsfläche parallele Ebene geclippt. Dabei müssen einige Sonderfälle beachtet werden die auftreten können, wobei der Fläche Punkte durch das Clipping hinzubekommt oder aber verliert. Die nachfolgende Abbildung 3.4 zeigt diese Fälle.
Liegen zwei benachbarte Punkte (siehe Abbildung 3.4 a)) hinter der Kamera so liegt zunächst keiner der obengenannten Sonderfälle vor. Liegt hingegen nur ein Punkt hinter der Kamera so wird durch das Clipping gegen die Ebene der Fläche ein Punkt hinzugefügt. Dargestellt ist dieser Fall in Abbildung 3.4 b). Erzeugt wird dieser zusätzliche Punkt durch die beiden Schnitte der Verbindungskanten mit der Begrenzungsebene. Liegen mehrere benachbarte Punkte hinter der Kamera, so können jene Punkte verworfen werden, die nicht mit einem Punkt vor der Kamera in Verbindung stehen. Dieser Fall wird in Abbildung 3.4 c) gezeigt.


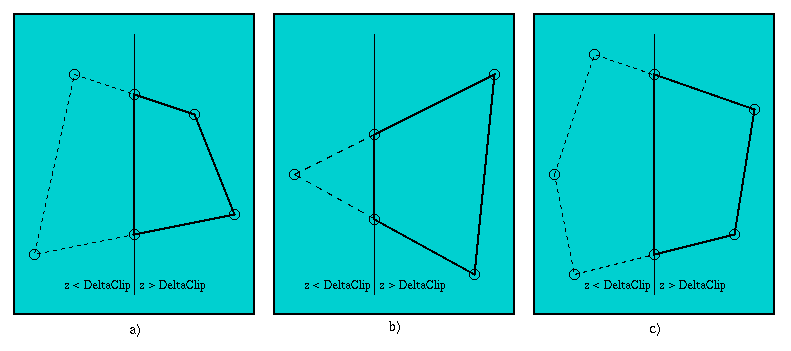
Abbildung 3.4: Fälle für das Clippen einer Fläche

Der Clipping-Algorithmus bewegt sich rund um die Fläche und testet dabei sukzessive jede der Kanten, ob sie gegen die Begrenzungsebene geclippt werden muß. Mit jedem Schritt wird einer zweiten Liste von Eckpunkten eine Anzahl von Eckpunkten hinzugefügt. Dieser Algorithmus ist ebenfalls in [Fole90, Seite 125f und Fig. 3.48] beschrieben. Es werden dabei die folgenden vier folgenden Fälle unterschieden:

StartpunktEndpunktPunkteintrag
z >= DeltaClipz >= DeltaClipEndpunkt
z < DeltaClipz >= DeltaClipSchnittpunkt der Kante mit der Begrenzungskante
z >= DeltaClipz < DeltaClipSchnittpunkt der Kante mit der Begrenzungskante,
anschließend Endpunkt
z < DeltaClipz < DeltaClipkein Punkt
Tabelle 3.1: Fälle für den Punkteintrag beim Clippen einer Fläche

3.3.2 Clippen gegen die Bildschirmkanten

Für das Clippen einer Fläche gegen den rechteckigen Bildschirm wird der in [Fole90, Seite 124ff] beschriebene Sutherland-Hodgman Polygon-Clip Algorithmus verwendet. Das Clippen gegen eine der vier Begrenzungskanten verläuft dabei nach dem gleichen Schema wie er für das Clippen gegen die zur Projektionsfläche parallele Ebene beschrieben wurde.
Im Unterschied zu dem vorher gezeigten Algorithmus wird die Fläche gegen jede der vier Begrenzungskanten getestet. In Anlehnung an den Cohen-Sutherland Linien-Clip Algoritmus [Fole90, Seite 113-117] wird dazu die Projektionsebene in vier unterschiedliche Regionen unterteilt. Jede dieser Regionen wird dabei durch ein Bit in einem 4-Bit Kode repräsentiert. Ein solches Bit wird gesetzt, falls der dem Kode zugeordnete Punkt in der entsprechenden Region liegt. Ein Punkt kann gleichzeitig in verschiedenen Regionen liegen, wobei sich einige natürlich durch deren gegensätzliche Lage ausschließen.
In der nachfolgenden Tabelle 3.2 sind Bits und ihre korrespondierenden Bedingungen aufgeführt.

Bit #RegionBedingung
0Obere Halbebene der oberen Begrenzungskantey < 0
1Rechte Halbebene der rechten Begrenzungskantex >= Breite
2Untere Halbebene der unteren Begrenzungskantey >= Höhe
3Linke Halbebene der linken Begrenzungskantex < 0
Tabelle 3.2: Bitzuordnung zu den Regionen

Weiter lassen sich aus den gesetzten Bits der Regionkodes der Eckpunkte Kriterien ableiten, mit deren Hilfe entschieden werden kann, ob das Polygon geclippt werden muß oder ob es sogar komplett verworfen werden kann. Liegen alle Punkte innerhalb des sichtbaren Bereichs der Projektionsebene ist für jeden Punkt der Regionenkode gleich Null und somit muß es nicht geclippt werden. Ist hingegen in den Regionenkodes der Eckpunkte das gleiche Bit gesetzt, kann die Fläche verworfen werden, da sie komplett in einer der äußeren, nicht sichtbaren, Regionen liegt. Liegt keine der beiden obengenannten Bedingungen vor, so muß die Fläche geclippt werden.
Mit Hilfe des Regionenkodes können die Bedingungen umformuliert werden, wie sie im Abschnitt 3.3.1 verwendet werden. so müssen die Bedingungen z >= DeltaClip durch (Region[Punkt] UND RegionBit) <> 0 und z < deltaClip durch (Region[Punkt] UND RegionBit) = 0. RegionBit ist dabei das Bit, welches der Begrenzungskante zugeordnet ist, gegen die die Fläche geclippt wird. Der Eintrag von Punkten erfolgt mit diesen neuen Bedingungen nach dem gleichen Schema, wie es im vorigen Abschnitt verwendet wurde (Tabelle 3.1).

3.3 Nachziehen der Flächenkanten

3.3.1 Bestimmen der nachzuziehenden Kanten

Bevor die Kanten nachgezogen werden, muß zuerst ermittelt werden, welche Kanten überhaupt nachgezogen werden müssen. Diese Problematik tritt dann auf, wenn ein Polygon an den Begrenzungen des Z-Buffer geclippt werden muß. So ist es in der folgenden Abbildung nicht notwendig, die durch das Clippen zusätzlich erzeugte Kante 2' nachzuziehen.


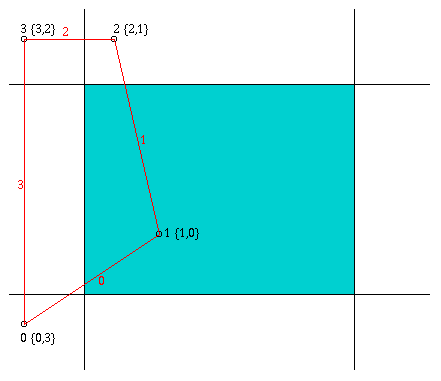
a) Ursprüngliches Polygon


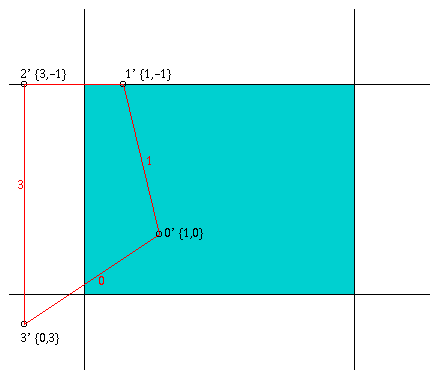
b) Clippen gegen y<=0


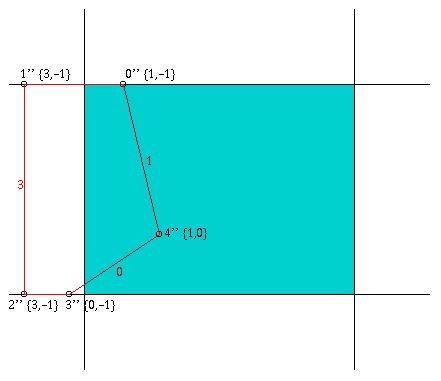
c) Clippen gegen y>Höhe


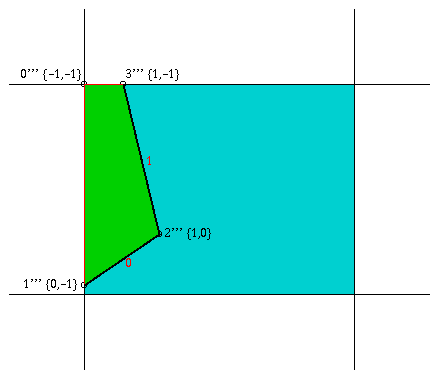
d) Clippen gegen x<=0
Abbildungen 3.4 a)-d): Bestimmung der nachzuziehenden Kanten

Für die Ermittlung, ob es notwendig ist, eine Kante nachzuzeichnen, wird ein Feld Edge verwendet, in dem zu jedem Eckunkt der Fläche, egal ob neu oder alt, verzeichnet wird, welche Kanten von ihm ausgehen und welche in ihm enden. Wird ein Punkt durch ein notwendiges Clippen an einer der Begrenzungskanten verschoben, so wird als Startkante diejenige Kante verzeichnet, auf der sich der Eckpunkt befindet. Für die endende Kante wird -1 in das Feldelement geschrieben. Dabei muß aber noch beachtet werden, ob der Punkt auf einer der ursprünglichen Kanten verschoben wird, oder ob er auf einer neu erzeugten Kante verschoben wird. Dies gilt für die in Abbildung 3.4 c und d bezeichneten Punkte 1'' und 0'''. Der Punkt 1'' wird entlang der oberen horizontalen Kante nach rechts in den neuen Punkt 0''' verschoben. Dies bedeutet, daß er sich nicht mehr auf einer ursprünglichen Kante (zuletzt Kante 3) befindet. Aus diesem Grund wird für die Startkante in dem Feld Edge der Wert -1 verzeichnet.

3.4 Korrektur in der Tiefenberechnung

Bei der Berechnung der Tiefe eines Flächen- oder Linienpunktes kann ein Fehler durch die Rasterisierung und die verwendeten Sichtstrahlen auftreten. Die folgende Abbildung 3.5 zeigt diesen Sachverhalt. Durch die Rasterisierung wird der linke Punkt auf den grünen Pixel projeziert, wobei sich der Schnittpunkt der Geraden Nullpunkt - linker Punkt in der rechten Teilhälfte des Pixels befindet. Bei der Tiefenberechnung wird nun eine Gerade vom Nullpunkt durch die Mitte des Pixels gelegt (siehe Kapitel 3.1 und 3.2). Diese Gerade schneidet die Fläche oder Linie links von deren Punkt, wodurch ein z-Wert entsteht, der außerhalb der durch die Fläche / Linie gegebenen z-Werte ZMin und ZMax liegt. Aus diesem Grund muß der z-Wert einer Fläche / Linie auf diesen Wert begrenzt werden.


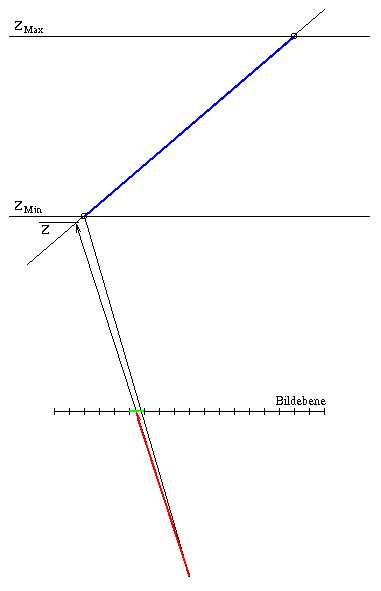
Abbildung 3.5: Fehler bei der Berechnung der Tiefe

4. Sichtbarkeitsprüfung von Merkmalen

Vorerst ist es nur möglich punkt- und linienförmige Merkmale zu verarbeiten. Der Test eines linienförmigen Merkmals beschränkt sich darauf den Punkt aus dem Weltsystem in das Kamerakoordinatensystem und anschließend in das Bildsystem zu transformieren. In der Bildebene kann die Sichtbarkeit des Punktes geprüft werden. Dazu muß der z-Wert des Punktes mit dem im Z-Frame befindlichen Wert verglichen werden. Ist der z-Wert des Punktes kleiner, so ist der Punkt sichtbar.
Bevor ein Linienmerkmal getestet werden kann, müssen die Endpunkte in das Koordinatensystem der Bildebene transformiert werden. Bei dieser Transformation müssen die gleichen Clipping-Verfahren verwendet werden, wie bei dem Clipping von Flächen. Dadurch wird gewährleistet, daß die auf die Bildschirmgrenzen geclippten Endpunkte des Linienmerkmals mit den geclippten Eckpunkten der Fläche übereinstimmen.
Da bei einem Linienmerkmal alle sich in der Bildschirmfläche befindlichen Linienpunkte auf ihre Sichtbarkeit getestet werden, kann das Merkmal in mehrere Liniensegmente zerfallen. Für die Berechnung der Segmentendpunkte wird eine Schnittberechnung durchgeführt, wie sie in Abbildung 4.2 und der nachfolgenden Herleitung gezeigt wird. Die nachstehende Abbildung 4.1 zeigt die notwendigen Schritte für den Test jedes Linienpunktes.


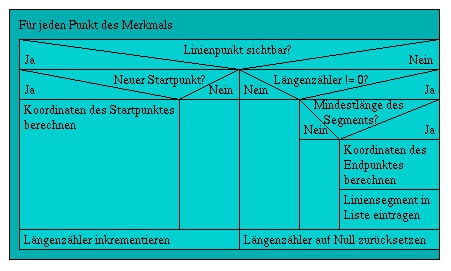
Abbildung 4.1: Testbedingungen für ein Linienmerkmal

Für die Berechnung eines Segmentendpunktes wird eine Schnittpunktberechnung zweier skalierter Vektoren durchgeführt. Der erste Vektor ist durch den Punkt gegeben, in dem eine Änderung der Sichtbarkeit auftritt (Vektor r in Abbildung 4.2). Dieser Vektor ist gegeben durch die Lage des Punktmittelpunktes im Bildschirm und daraus resultierend dessen Lage im Kamerasystem. Der zweite Vektor ist definiert durch das Linienmerkmal im Kamerasystem als Verbindungsvektor vom Start- zum Endpunkt (v in Abbildung 4.2). Ausgeführt wird die Schnittpunktberechnung dabei aber immer in einer 2-dimensionalen Projektion, da ein Schnitt im 3-dimensionalen im allgemeinen nicht möglich ist, weil die durch die Vektoren definierten Geraden windschief stehen können und dies im allgemeinen auch so ist. Aus diesem Grund wird immer die Projektion auf die xz- oder yz-Ebene verwendet, je nachdem in welcher Projektion sich der Verbindungsvektor v am stärksten ändert, d.h. welcher der beiden Werte vx oder vy größer ist.


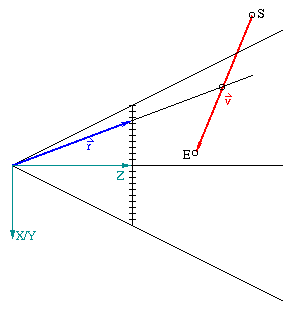
Abbildung 4.2: Berechnung eines Segmentendpunktes

O + a·r = S + b·v

Diese Gleichung läßt sich nun in ein 2-dimensionales Gleichungssystem überführen:

a·rx/y = Sx/y + bvx/y
a = Sz + bvz

Durch Auflösen nach b kann der Schnittpunkt aus dem zweiten Teilterm der ersten Gleichung berechnet werden. Der Schnittpunkt liegt sodann in Kamerakoordinaten vor. Für b ergibt sich folgende Gleichung:

Sx/y - Sz·rx/y
b =  ------------
vz·rx/y - vx/y

Um zu gewährleisten, daß bei dem Ziehen von Linien in beiden Richtungen die gleichen Punkte erzeugt werden, wird die Linie immer in positiver y-Richtung gezeichnet. Dadurch kann es notwendig sein, Start- und Endpunkt des Linienmerkmales zu vertauschen. Dies gilt es bei dem Erzeugen der Liste für die sichtbaren Liniensegmente zu beachten: Im Normalfall werden die neuen Segmente an die Liste angehängt und die Start- und Endpunkte entsprechend in die Segmente eingetragen. Wurden der Start- und Endpunkt des Linienmerkmals vertauscht, muß hingegen das neue Segment an den Anfang der Liste gestellt werden, und der Start- und Endpunkt muß in den End- bzw. Startpunkt des Segments eingetragen werden. Auf diese Weise wird sichergestellt, daß die Orientierung der Segmente der Orientierung des Linienmerkmals entsprechen.

5. Die Klasse ZBuffer und ihre Accessoren

5.1 Klassenableitung

Die Klasse ZBuffer ist von der Klasse RectI public abgeleitet.

5.2 Klassendefinition

class ZBuffer : public RectI

5.3 Kostruktoren

5.4 Destruktor

5.5 Operatoren

5.6 Methoden

Anhang

A. Flußdiagramme

A.1 Flußdiagramm der Methode Add( gs_Face3D& face)

Die Methode ZBuffer& Add( gs_Face3D& face ) trägt eine Fläche in den Z-Buffer ein. Dazu wird die Fläche verschiedenen Bearbeitungsschritten unterzogen. Die wichtigsten dabei sind die Transformation in das Kamerakoordinatensystem und Sichtbarkeitstests (Backface-Culling), sowie die Begrenzung der Fläche in seiner Ausdehnung hinter die Kamera.
Daraufhin können die Eckpunkte in das Bildschirmkoordinatensystem transformiert werden. Es folgen Tests, ob die Fläche gegen die Ränder des Bildschirms geclippt werden muß.
Nachfolgend werden die Punkte der Begrenzungskanten der Fläche bestimmt. Nachdem dies erfolgt ist, wird die Fläche gefüllt und zuletzt die sichtbaren Teile der ursprünglichen Flächenkanten nachgezeichnet.


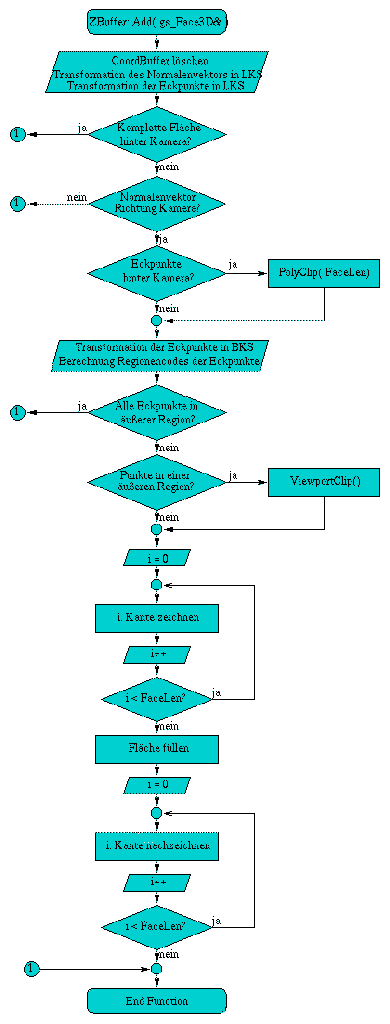
Abbildung A.1: Flußdiagramm der Methode Add( gs_Face3D& face)

A.2 Flußdiagramm der Methode PolyClip( int& facelen )

Die Methode int PolyClip( int& facelen ) begrenzt eine Fläche in seiner Ausdehnung hinter die Kamera. Dazu wird das Polygon mit einer Fläche geschnitten, die sich im Abstand DeltaClip vor der x-y-Ebene des lokalen Systems befindet. Wichtig ist dabei die Verwendung von zwei getrennten Feldern, in denen die Eckpunkte der Fläche gespeichert werden. Zu diesem Zweck wird ein 2-dimensionales Feld VectArray[2][MAXVERTICES] verwendet, in dem abwechselnd die Eckpunkte gespeichert werden können. Die Umschaltung zwischen den beiden Feldern geschieht durch die beiden Variablen ActArray und newarray. Für das Eintragen eines Eckpunktes in das neue Feld wird die Variable newlen verwendet.
Am Schluß der Funktion wird die übergebene Referenz facelen mit der neuen Anzahl von Eckpunkten des Polygons newlen überschrieben. Die Variable ActArray gibt an, in welchem Feld sich die aktuellen Eckpunkte der Fläche befinden und wird zurückgegeben.


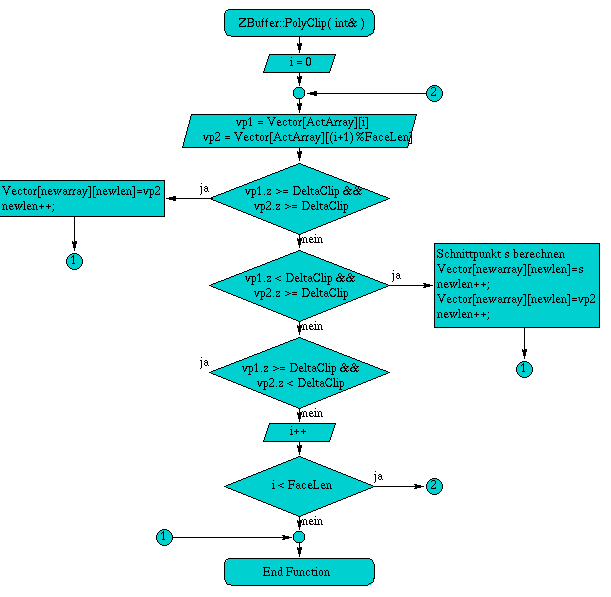
Abbildung A.2: Flußdiagramm der Methode PolyClip( int& facelen )

A.3 Flußdiagramm der Methode ViewportClip( int& facelen )

Die Methode int ViewportClip( int& facelen ) begrenzt eine Fläche in der Bildebene. Dazu wird die Fläche nacheinander gegen die einzelnen Bildschirmkanten, so daß am Ende nur die sichtbaren Bereiche der Fläche übrigbleiben. Für die Bestimmung ob die Fläche gegen eine der Begrenzungskanten geclippt werden muß, wird für jeden Eckpunkt ein Regionencode verwendet, der seine Lage definiert.
Wird ein Eckpunkt aufgrung des Clippings entlang einer Kante verschoben, so wird das Feld Edge neu berechnet, ebenso werden die Regionen neu bestimmt.





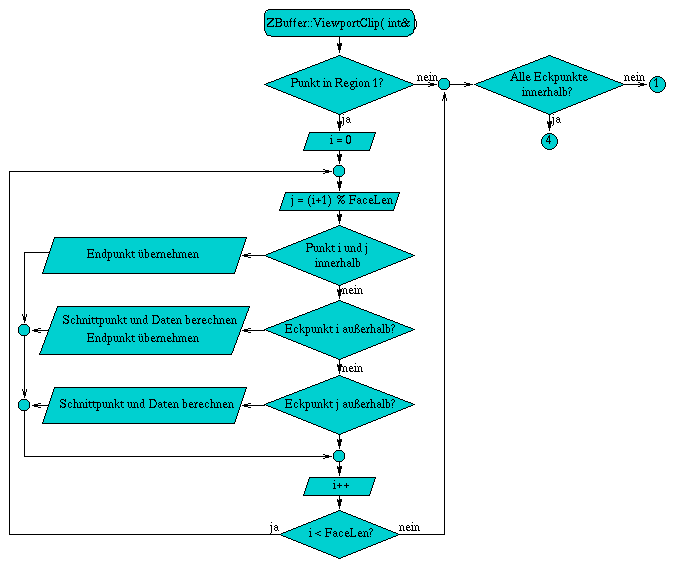
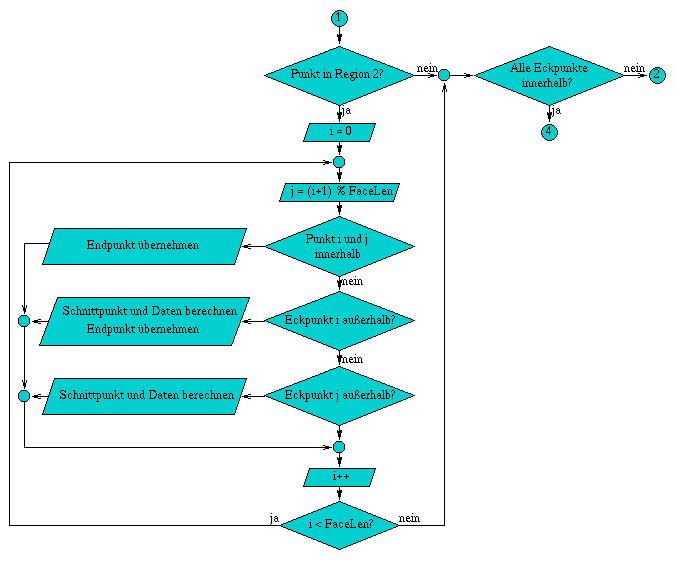
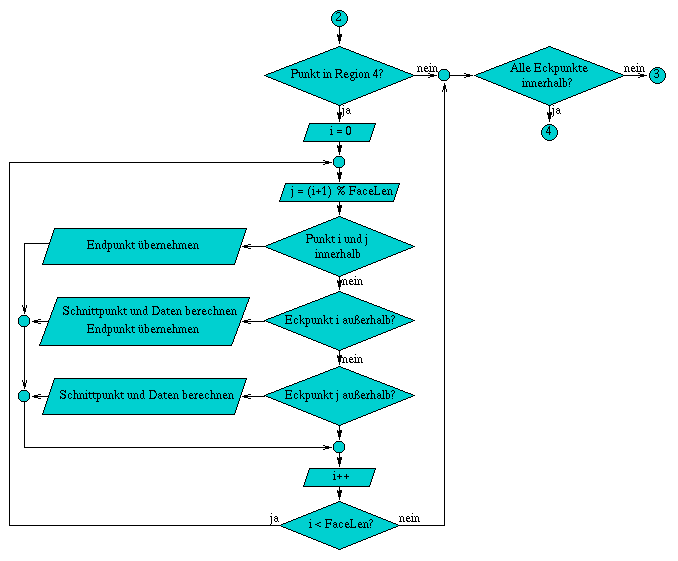
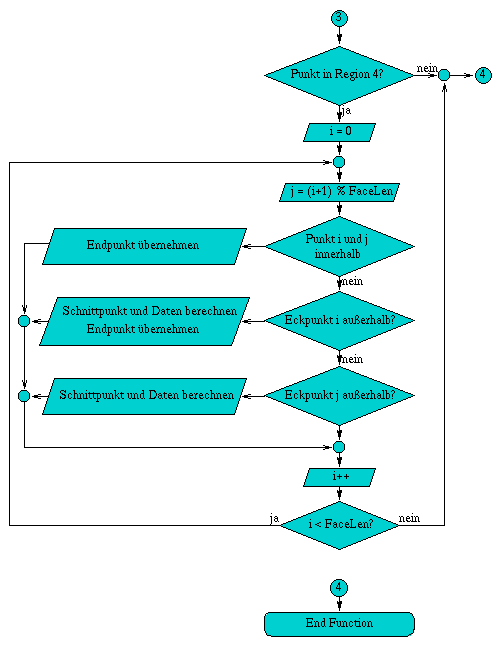
Abbildung A.3: Flußdiagramm der Methode ViewportClip( int& facelen )

A.4 Flußdiagramm der Methode PolyEdge( Vector3D& start, Vector3D& end, ID id )

Die Methode void PolyEdge( Vector3D& start, Vector3D& end, ID id ) berechnet die Linienpunkte einer Kante und registriert deren x- und y-Werte. Die Linienpunkte werden dabei nach dem Algorithmus von Bresenham berechnet (Siehe [Fole90], Seiten 74-81).


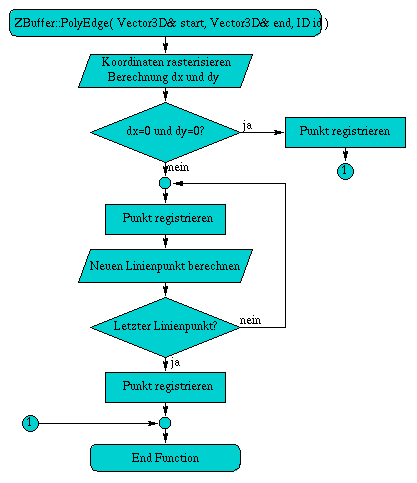
Abbildung A.4: Flußdiagramm der Methode PolyEdge( Vector3D& start, Vector3D& end, ID id )

A.5 Flußdiagramm der Methode UpdateEdge( int start, int end, ID id, int facelen )

Die Methode void UpdateEdge( int start, int end, ID id, int facelen ) testet zunächst, ob es überhaupt notwendig ist die Kante nachzuzeichnen. Dies geschieht mit der in Abschnitt 3.3 beschriebenen Methode. Darauffolgend wird für jeden Punkt der Kante geprüft, ob dieser mit dem im Id-Frame eingetragenen Id-Wert übereinstimmt, ist dies der Fall wird der Tiefenwert des Punktes neu berechnet und in den Z-Frame eingtragen. Für die Berechnung der Linienpunkte wird ebenfalls der Algorithmus nach Bresenham verwendet.


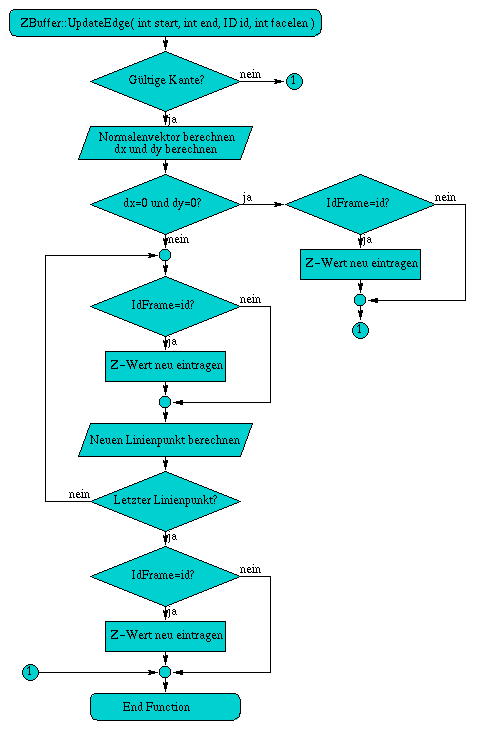
Abbildung A.5: Flußdiagramm der Methode UpdateEdge( int start, int end, ID id, int facelen )

A.6 Flußdiagramm der Methode TestVis( const Line3D& line )

Die Methode ZBuffer& TestVis( const Line3D& line ) test als erstes, ob sich die komplette Linie hinter der Kamera befindet, wodurch es unnötig ist die Linie weiter zu testen. Daraufhin folgen die beiden Varianten des Clippings, falls diese notwendig sind. Zuerst wird gegen die zur xy-Ebene parallele Ebene im Abstand z = DeltaClip geclippt, Daraufhin erfolgt das Clippen gegen die Begrenzungen des Bildschirms. Wurde die Linie in ihren Ausmaßen auf die Projektionsfläche begrenzt, können die rasterisierten Linienpunkte auf ihre Sichtbarkeit geprüft werden.








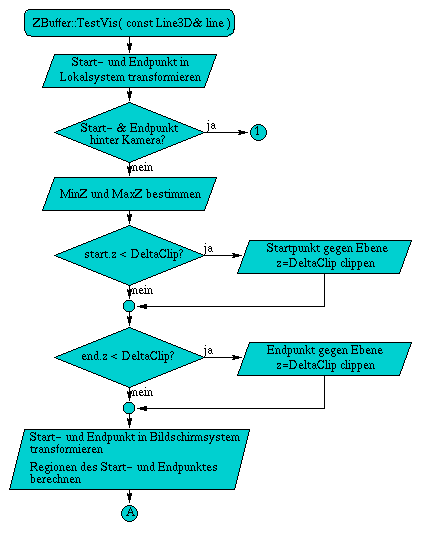
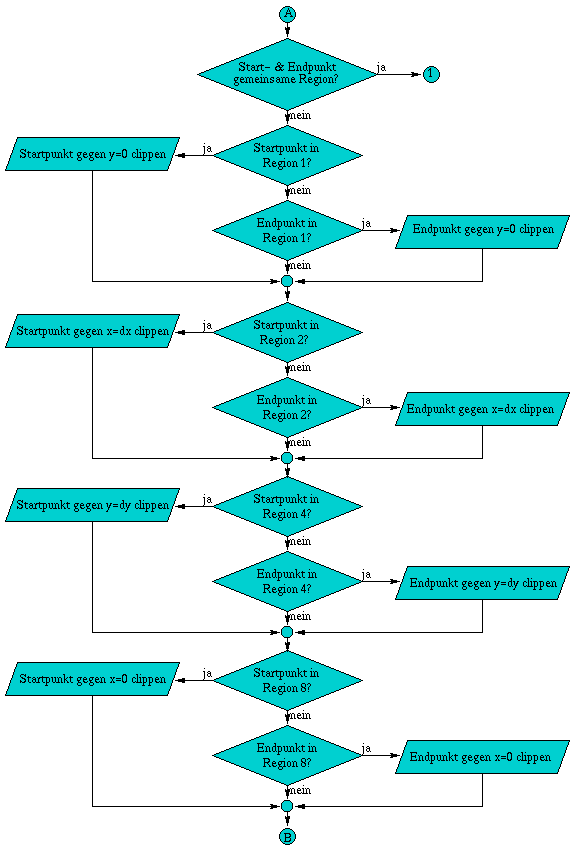
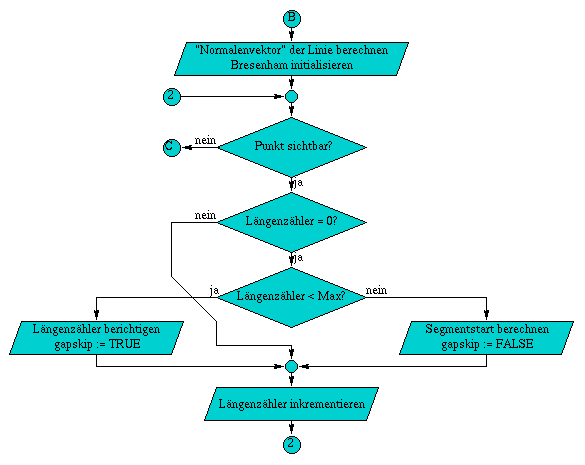
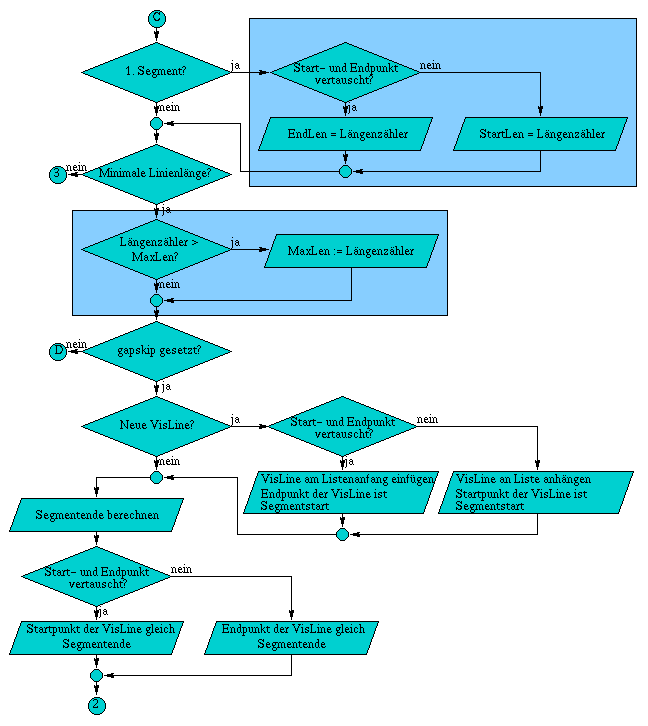
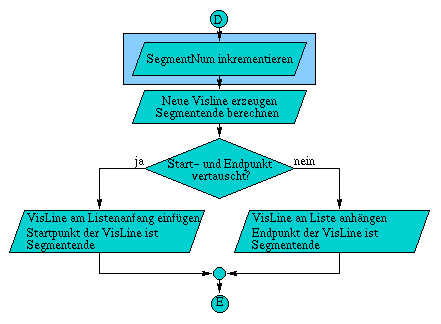
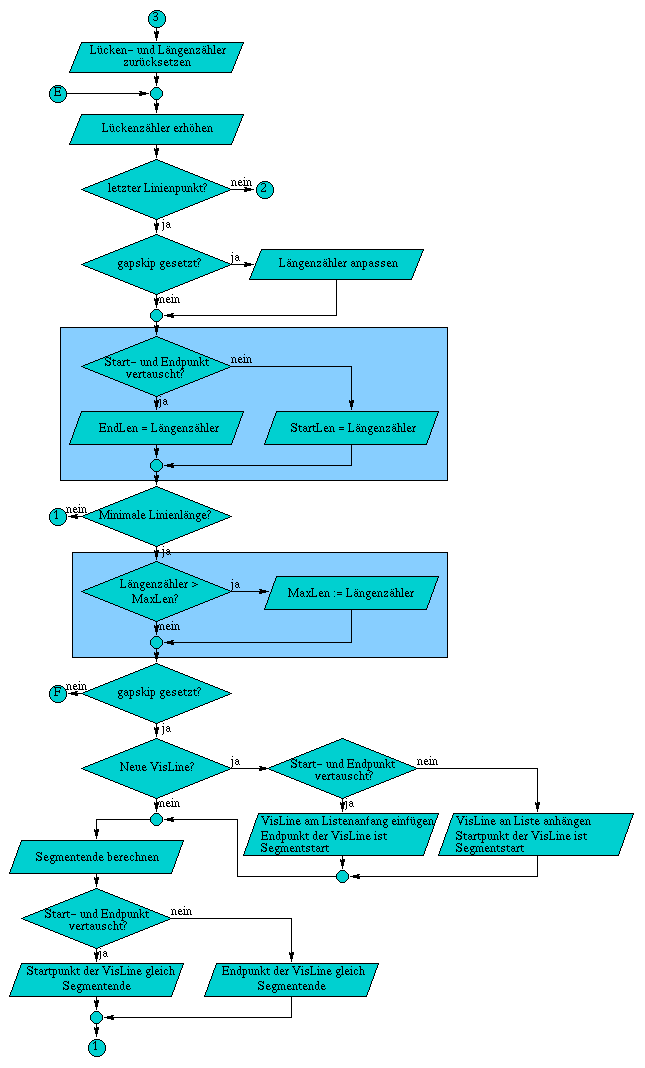
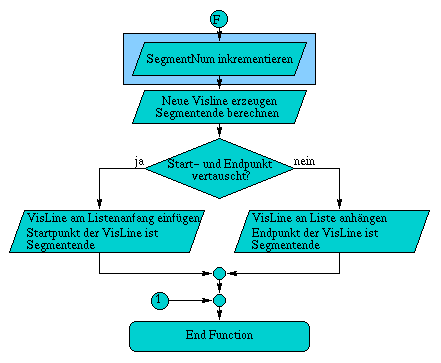
Abbildung A.6: Flußdiagramm der Methode TestVis( const Line3D& line )

Literaturverzeichnis


[Lenz87]Lenz, Reimar:
Linsenfehlerkorrigierte Eichung von Halbleiterkameras mit Standardobjektiven für hochgenaue 3-D-Messungen in Echtzeit
Lehrstuhl für Nachrichtentechnik, TU München
Mustererkennung, Informatik Fachberichte 149
Berlin: Springer, 1987
[Fole90]Foley, James - van Damm, Andries - Feiner, Steven - Hughes, John:
Computer Graphics
Principles and practice
New York: Addison - Wesley, 1990
Stefan Unterholzner
Lehrstuhl für Prozessrechner
Technische Universität München
$Id: zbuffer.html,v 1.3 1996/03/27 18:25:30 uholzner Exp uholzner $